生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。


今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。

 

 

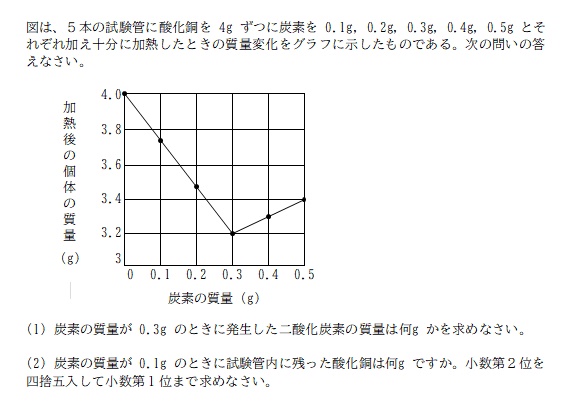
(1)

 

炭素 0.3g の試験管について考える。

 

酸化銅 4.0g に炭素 0.3g を入れているので、試験管内の物質の質量は 4.3g となる。それを加熱し終えたら 3.2g になっていたので、加熱前→加熱後で消失した 4.3 - 3.2 = 1.1g が二酸化炭素の質量であると考えられる。

 

A. (1) 1.1g

 

 

ちなみに、炭素の質量が 0.1g ～ 0.3g までは右下がり、0.4g ～ 0.5g が右上がりのグラフになっているのは、炭素 0.3g で酸化銅の中の酸素すべてと反応しきってしまい余った炭素が試験管内に残るから。

 

酸化銅 4.0g の中の銅と酸素の質量は、

 

　銅：酸素：酸化銅 = 4：1：5

　　　　　　　　　 = 3.2g：0.8g：4.0g

 

となるので、炭素 0.3g の試験管の実験では、炭素 0.3g と酸素 0.8g すべてが反応し二酸化炭素 1.1g となって消失、銅 3.2g だけが試験管内に残った、ということになりますね。

 

なので炭素の量を 0.3g から増やしても、増やした炭素と反応するだけの酸素はもうないので、二酸化炭素となって消失する量も変わらず 1.1g のまま。

 

　炭素 0.4g の試験管

　→酸素 0.8g と炭素 0.3g が反応し二酸化炭素 1.1g となって消失、

　　銅 3.2g と余った炭素 0.1g の計 3.3g が試験管内に残った。

 

　炭素 0.5g の試験管

　→酸素 0.8g と炭素 0.3g が反応し二酸化炭素 1.1g となって消失、

　　銅 3.2g と余った炭素 0.2g の計 3.4g が試験管内に残った。

 

となるので、炭素 0.3g 以降のグラフは右上がりのグラフになっているということ。

 

問題を解くだけではなく、こんな感じできちんと理解していれば還元反応の様々なパターンの出題に対応できると思います。

 

 

 

(2)

 

炭素 0.1g ということは、炭素 0.3g の「３分の１」だということ。

考え方はとてもシンプルです。

 

つまり、反応した酸化銅の質量も「３分の１」ということになり、反応せずに残った酸化銅の質量は「３分の２」ということになりますね。

 

　4.0 × 2/3 = 2.666･･･ ≒ 2.7

 

A. (2) 2.7g

 

 

ちなみに炭素 0.1g の試験管ですが、「加熱後の個体の質量」をグラフで見ると 3.7g よりちょっと多いくらいのところを通っていますね。

 

「あれ？試験管内に残った酸化銅の質量って 2.7g なのに何で？」って思った人は勉強のチャンスです！

 

 

試験管内に残った「加熱後の個体の質量」が何を指しているか。これは、

 

「炭素と反応し還元されて残った銅の質量 + 炭素と反応せずに残った酸化銅の質量」

 

となります。

 

 

問題 (2) の解は「炭素と反応せずに残った酸化銅の質量」なので、「炭素と反応し還元されて残った銅の質量」について求める必要がありますね。反応した酸化銅の質量も「３分の１」なので、

 

　4.0 × 1/3 = 1.333･･･

 

この酸化銅の質量 1.333･･･g に含まれる銅と酸素それぞれの質量を求めます。

 

　銅：酸素：酸化銅 = 4：1：5

　　　　　　　　　 = 1.066･･･g：0.266･･･g：1.333･･･g

 

質量 1.333･･･g の酸化銅に含まれる酸素 0.266･･･g と反応し還元されて銅 1.066･･･g が残った、ということになりますね。

 

よってグラフの点、炭素 0.1g の試験管の「加熱後の個体の質量」は、

 

　1.066･･･ + 2.666･･･ = 3.733･･･

 

という値になり、グラフの点の位置とも合致することが分かります。

 

 

炭素 0.2g のときの値についても求めて、炭素 0.1g ～ 0.5g それぞれの各種値もすべてまとめて整理してみました。

 

 

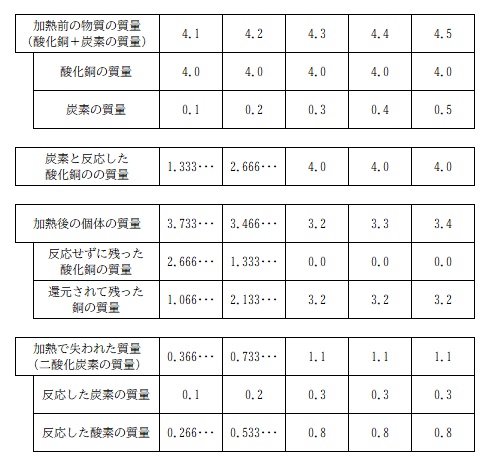
勉強の参考までに。多分あってると思います。解答があるわけではないので確認はできませんが、何回も計算して確認したので。

 

 

問題で問われている内容に対してだけ答えを出して、ハイ終わり、ではなく、分からないことがひとつも残ってない！ってくらいまでとことん考えて、完璧に理解しようって努力する。これが勉強だと私は思っています。

 

(1)(2) のたった２つの問題でもこれだけ色々なことを学ぶことができるんですね。

 

 

ここまでやれば、酸化銅の還元、もちろん酸化銅以外であってもですが、どんなパターンの出題があっても解くだけの力が付くのではないかと思います！

 

 

-----

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾

 

生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、6/28 と 6/29 に投稿した記事の問題の別解についてです。

 

 

※問題の全文は、一昨日の記事（「分からない」を考えよう！ #11）を参照ください。

 

 

一昨日の記事に書いた考え方でも良いのだけれど、「鉄粉と銅粉の混合物」「硫化鉄と硫化銅の混合物」の質量がもっと大きな値になった場合はあの解き方だときっと大変なんですよね。

 

なので、記事を書いた後もずっと他の解き方を考えていたのですが、昨夜寝る前にふと閃いたので解説したいと思います。

 

 

(4)

 

鉄と硫化鉄、銅と硫化銅、それぞれの比率を元に考える。

 

　鉄：硫化鉄 = 7：11

　銅：硫化銅 = 2：3

 

硫黄については「十分な量を混ぜ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、鉄粉と銅粉の混合物が 20g、硫化鉄と硫化銅の混合物が 31g になるように考える。

 

ここまでは同じ。

 

 

鉄と硫化鉄の比率を変えずに質量を調整したい場合、両方を同じ倍率で増減させればいいが、その「何倍すればいいか」が分からない。なので、その倍率を x として考えれば良い。

 

銅と硫化銅も同様。こちらの倍率は y として考える。

 

　鉄：硫化鉄 = 7：11 ← x倍する

 

　銅：硫化銅 = 2：3 ← y倍する

 

　鉄：硫化鉄 = 7x：11x

 

　銅：硫化銅 = 2y：3y

 

それぞれ必要な質量をこのように表すことができる。

 

 

　鉄粉と銅粉の混合物が 20g なので、

 

　7x + 2y = 20

 

　硫化鉄と硫化銅の混合物が 31g なので、

　11x + 3y = 31

 

あとはこの二つの式を連立方程式で解けば、それぞれの倍率を求めることができる。

計算についてはここでは割愛。

 

　x=2 , y=3

 

計算結果はこのようになるので、

 

　鉄：硫化鉄 = 7×2：11×2

　　　　　　 = 14g：22g

 

 

　銅：硫化銅 = 2×3：3×3

 

　　　　　　 = 6g：9g

 

倍率を代入すればそれぞれの質量を求めることができます。この問題は「混合物 20g の中の鉄粉の質量」を求める問題なので、

 

 

A. (4) 14.0g

 

 

 

 

※問題の全文は、昨日の記事（「分からない」を考えよう！ #12）を参照ください。

 

 

こちらの問題も考え方は全く同じ。前に問題の解説を読んで「分かった！」と思えたのなら、この問題の解説を読む前に、ぜひ自分の力で解いてみてください！

 

 

(3)

 

銅と酸化銅、マグネシウムと酸化マグネシウム、それぞれの比率を元に考える。

 

　銅：酸化銅 = 4：5

　マグネシウム：酸化マグネシウム = 3：5

 

酸素については「十分に酸素と化合させ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、銅とマグネシウムの混合物が 3.1g、酸化銅と酸化マグネシウムの混合物が 4.5g になるように考える。

 

 

銅と酸化銅の比率を変えずに質量を調整したい場合、両方を同じ倍率で増減させればいいが、その「何倍すればいいか」が分からない。なので、その倍率を x として考えれば良い。

 

マグネシウムと酸化マグネシウムも同様。こちらの倍率は y として考える。

 

　銅：酸化銅 = 4：5 ← x倍する

 

　マグネシウム：酸化マグネシウム = 3：5 ← y倍する

 

　銅：酸化銅 = 4x：5x

 

　マグネシウム：酸化マグネシウム = 3y：5y

 

それぞれ必要な質量をこのように表すことができる。

 

 

　銅とマグネシウムの混合物が 3.1g なので、

 

　4x + 3y = 3.1

 

　酸化銅と酸化マグネシウムの混合物が 4.5g なので、

　5x + 5y = 4.5

 

あとはこの二つの式を連立方程式で解けば、それぞれの倍率を求めることができる。

計算についてはここでは割愛。

 

　x=0.4 , y=0.5

 

計算結果はこのようになるので、

 

　銅：酸化銅 = 4×0.4：5×0.4

　　　　　　 = 1.6g：2.0g

 

 

　マグネシウム：酸化マグネシウム = 3×0.5：5×0.5

 

　　　　　　　　　　　　　　　　 = 1.5g：2.5g

 

倍率を代入すればそれぞれの質量を求めることができます。この問題は「元の混合物 3.1g の中のマグネシウムの質量」を求める問題なので、

 

 

A. (3) 1.5g

 

 

 

 

このように問題の解き方っていうのはひとつではないし、さまざまな考え方で解くことができたりします。

 

ひとつの解き方が分かったとしても、何か納得できないひっかかりが少しでも残っているなら「何か他にもっといい解き方、考え方はないだろうか」って突き詰めてみるのも楽しいものです！

 

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 
以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾

 

生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。


今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。

 

 

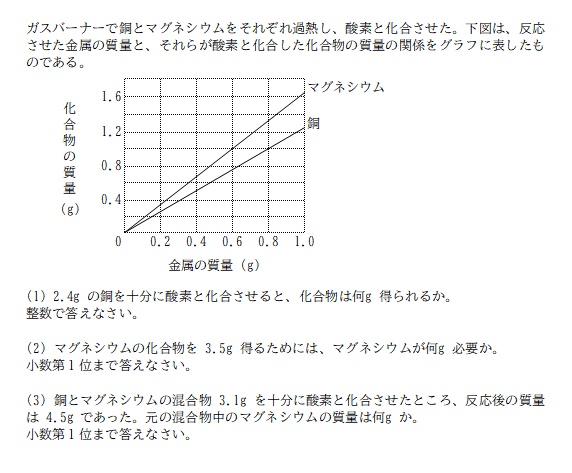
昨日の記事（「分からない」を考えよう！ #11）を読んで「分かった！」と思えたなら解ける問題です。

 

勉強は「分かった！」と思っただけでは終わりではありません。「分かった！」と思ったなら、それが本当なのかどうかを確認し「分かった！、ということを証明する」ところまでやってはじめて勉強したといえます。

 

本当に「分かった！」のか、「分かった気になった」だけなのか、その確認のためにもぜひチャレンジしてみてください。

 

 

(1)

 

グラフから必要な情報を読み取ります。

縦線と横線の交点を銅のグラフが通る場所を探すと、金属の質量 0.8g / 化合物の質量 1.0g の点を通っていることが分かる。

 

銅 0.8g が酸化し、酸化銅 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。

 

　銅：酸化銅 = 0.8：1.0

　　　　　　 = 8：10

　　　　　　 = 4：5

 

この比率を利用して銅 2.4g に対する酸化銅の質量を求めれば良い。

 

　銅：酸化銅

　4：5 = 2.4：x

　4x = 12

　x = 3

 

A. (1) 3.0g

 

 

(2)

 

これも先の問題同様、グラフから必要な情報を読み取ります。

縦線と横線の交点をマグネシウムのグラフが通る場所を探すと、金属の質量 0.6g / 化合物の質量 1.0g の点を通っていることが分かる。

 

マグネシウム 0.6g が酸化し、酸化マグネシウム 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。

 

　マグネシウム：酸化マグネシウム = 0.6：1.0

　　　　　　　　　　　　　　　　 = 6：10

　　　　　　　　　　　　　　　　 = 3：5

 

この比率を利用して酸化マグネシウム 3.5g の元になったマグネシウムの質量を求めれば良い。

 

　マグネシウム：酸化マグネシウム

　3：5 = x：3.5

　5x = 10.5

　x = 2.1

 

A. (2) 2.1g

 

 

(3)

 

銅と酸化銅、マグネシウムと酸化マグネシウム、それぞれの比率を元に考える。

 

　銅：酸化銅 = 4：5

　マグネシウム：酸化マグネシウム = 3：5

 

酸素については「十分に酸素と化合させ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、銅とマグネシウムの混合物が 3.1g、酸化銅と酸化マグネシウムの混合物が 4.5g になるように考える。

 

ここからは分かりやすいように、

 

　銅とマグネシウムの混合物 3.1g → 31g

　酸化銅と酸化マグネシウムの混合物 4.5g → 45g

 

というように 10倍した値で考ることにします。

 

銅+マグネシウムが 31g (奇数) ということは、銅 (偶数) + マグネシウム (偶数) という組み合わせにはならないことが分かる。銅「4」は何倍しても偶数なので、マグネシウム「3」の方を奇数にするよう考える。

 

銅：酸化銅、マグネシウム：酸化マグネシウム、の比率をそのまま質量として、銅とマグネシウムの混合物 31g、酸化銅と酸化マグネシウムの混合物 45g になる組み合わせを探していく。

 

　マグネシウム：酸化マグネシウム = 3g：5g

 

　　11倍すると 33g：55g → どちらも問題文にある値を超えるので NG

 

　　9倍すると 27g：45g → これだと酸化マグネシウムが問題文にある値を超えるので NG　

 

　　7倍すると 21g：35g

　　　→ (銅：酸化銅 = 4g：5g) を 2.5倍した (10g：12.5g) を混ぜ合わせると

　　　　31g：47.5g となるので NG

 

　　5倍すると 15g：25g

　　　→ (銅：酸化銅 = 4g：5g) を 4倍した (16g：20g) を混ぜ合わせると

　　　　31g：45g となるのでこの割合で混ぜ合わせるのが正解！

 

となり問題文と合致する質量を求めることができましたね。31g と 45g は本来の質量を考えやすいように 10倍にした値なので、

 

　銅：酸化銅 = 1.6g：2.0g

　マグネシウム：酸化マグネシウム = 1.5g：2.5g

 

で混ざり合っていると考えることができる。よって元の混合物中のマグネシウムの質量は、

 

A. (3) 1.5g

 

 

いかがでしたか？

 

 

前回の記事を読んで、その問題を解く考え方をちゃんと理解できていたなら、今回の問題も解くことができるはずです。

 

解くことができないということは、残念ながら前回の記事の問題を「ちゃんと理解できていなかった」可能性が高い、ということになります。

 

最初にも書きましたが、「分かったと思う」ことがひとつの勉強のゴールではないです。「分かったと思ったことを、本当に分かったのか確認し証明する」ことまでやってはじめてひとつの勉強のゴールだと言えるのです。

 

問題が解けて分かったと思えたなら、必ずその類題を探してチャレンジするようにしてくださいね！

 

 

-----

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 
以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾

 

生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。


今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。

 

 

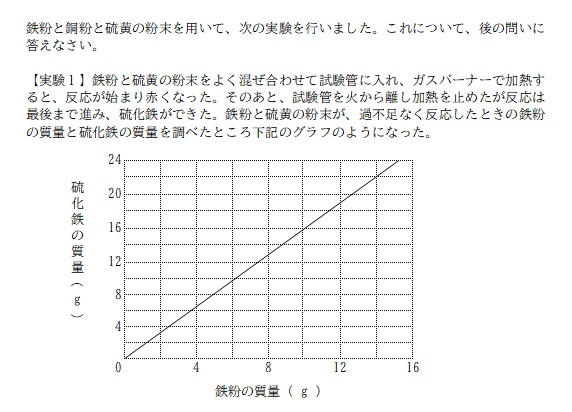
今回から、記事の構成や書き方をこれまでとは変えて、できるだけシンプルに、なるべく短く、を心がけて書いていきます。

 

 

(1)

 

グラフから必要な情報を読み取ります。

縦線と横線の交点をグラフが通る場所を探すと、鉄粉 14g / 硫化鉄 22g であることが分かる。

 

そこから反応した硫黄の質量を求めると、22-14＝8 で、硫黄 8g となる。

 

これらの情報から３つの物質の質量比を求めると、

 

　鉄：硫黄：硫化鉄 = 14：8：22

　　　　　　　　　 = 7：4：11

 

となる。あとはこの比率を利用して硫化鉄 16.5g に対する硫黄の質量を求めれば良い。

 

　硫黄：硫化鉄

　4：11 = x：16.5

　11x = 66

　x = 6

 

A. (1) 6.0g

 

 

(2)

 

この問題も (1) で使った「鉄/硫黄/硫化鉄」の比率を使って解くことができる。

 

気を付けるポイントは、鉄粉 26.8g が全て反応したのか、一部が反応し余りが出たのか、という点。もちろん、硫黄 12.0g について同様に考えても良い。

 

ここの意味が分かっていないと 26.8+12.0=38.8g の硫化鉄！みたいな間違った回答をすることになる。

 

ますは、鉄粉 26.8g が完全に反応するのに必要な硫黄の質量を考えてみる。

 

　鉄：硫黄

　7：4 = 26.8：x

　7x = 107.2

　x = 15.3･･･

 

となるので、鉄粉 26.8g が完全に反応するには硫黄 12.0g だけだと少し足りないことが分かる。言い方を変えると、この硫黄の量では鉄粉は全て反応せず余る、ということ。

 

つまり、鉄粉 26.8g が全て反応して何g の硫化鉄になるか、ではなく、硫黄 12.0g が全て反応して何g の硫化鉄になるか、を考えれば良い。

 

　硫黄：硫化鉄

　4：11 = 12：x

　4x = 132

　x = 33

 

 

A. (2) 33.0g

 

 

(3)

 

実験２の問題文に書いてある、銅と硫化銅の質量から反応した硫黄の質量を求め、それらの情報から３者の質量の比率を求める。

 

　硫化銅 5.1 - 銅 3.4 = 硫黄 1.7

 

　銅：硫黄：硫化銅 = 3.4：1.7：5.1

　　　　　　　　　 = 2：1：3

 

銅の原子と硫黄の原子が１：１で結びつく、と記載があるので上記の質量比率がそのまま原子１個の質量比率となることが分かる。

 

問題 (1) で求めた鉄/硫黄/硫化鉄の質量比率、

 

　鉄：硫黄：硫化鉄 = 7：4：11

 

これも上記の質量比率がそのまま原子１個の質量比率となる。問題文を読んでも鉄の原子と硫黄の原子の結びつきが１：１という記述はないが、硫化鉄の化学反応式「Fe+S→FeS」を知っていれば考えることができる。

 

ここまでで、銅と硫黄、鉄と硫黄、それぞれの原子１個の質量比率が分かったが、銅と鉄の質量比率を求めるには２つの比率の中で共通する硫黄の比率を揃えて比較する必要があるので、

 

　鉄：硫黄 = 7：4

　銅：硫黄 = 2：1 ← こっちを 4倍して硫黄の比率を揃える

 

 

　鉄：硫黄 = 7：4

　銅：硫黄 = 8：4

 

よって、鉄の原子１個と銅の原子１個の質量の比は 7：8 となる。

 

A. (3) 7：8

 

 

 

 

(4)

 

鉄と硫化鉄、銅と硫化銅、それぞれの比率を元に考える。

 

　鉄：硫化鉄 = 7：11

　銅：硫化銅 = 2：3

 

硫黄については「十分な量を混ぜ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、鉄粉と銅粉の混合物が 20g、硫化鉄と硫化銅の混合物が 31g になるように考える。

 

鉄+銅が 20g (偶数) ということは、鉄 (奇数) + 銅 (偶数) という組み合わせにはならないことが分かる。銅は何倍しても偶数なので、鉄の方を偶数にするよう考える。

 

鉄が 7 の 4倍だと 28 となり問題文の 20g を超えてしまうので使えるのは 2倍の 14g しかないと考えることができる。そこに銅を加えて 20g にするには、銅 2 を 3倍して足せば良い。

 

　鉄：硫化鉄 = 7：11 ← 2倍

　銅：硫化銅 = 2：3 ← 3倍

 

　鉄：硫化鉄 = 14：22

　銅：硫化銅 = 6：9

 

これで混ぜ合わせると、

 

　鉄+銅：硫化鉄+硫化銅 = 20：31

 

となり問題文と合致する質量を求めることができましたね。よって鉄と銅の混合物の中の鉄の質量は 14g であると分かります。

 

A. (4) 14.0g

 

 

 

 

 

いかがでしたか？

 

私だったらこんな風に考えて解くかな、という解説です。他にも解き方、考え方はいろいろあると思います。そういうのを考えたり調べて勉強するのも面白いかもしれません。

 

特別な化学の知識がないと解けない、というような問題ではなく、問題の中の情報を整理し考えれば解ける問題だと思います。個人的にはこういう「考えれば解ける問題」は好きですね。

 

 

-----

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾

 

生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、とある中学の授業で出されたプリントからの出題、理科(2年 化学) の問題です。

 

どこかの高校入試の問題の引用らしく、(6) が難しいと言って生徒が持ってきてくれた問題です。

 

 

-----

まずは (1) から。この問題は、銅と酸化銅の質量の変化を示した表のデータから計算して求めることができますね。それでは！

 

Let's think!

 

(1) の問題。

10.0g の銅を完全に酸素と反応させると何g の酸化銅になるか。表に書かれている銅と酸化銅の質量から比率を求めて、そこに 10.0g を当てはめるとどうなるか、を考えれば良いですね。

 

表より、銅 0.4g → 酸化銅 0.5g ということが読み取れるので、銅と酸化銅の比率は、

 

　銅：酸化銅 = 0.4：0.5 = 4：5

 

ということが分かります。あとは比例式にして計算します。

 

ちなみに比例式の計算の仕方について。「内項の積と外項の積は等しい」という性質から

A:B=C:D → AD=BC

となるのですが、分からない子は調べて勉強しなおしておきましょう。

 

　4：5 = 10.0：x

　4x = 50.0

　x = 12.5

 

よって、10.0g の銅を完全に酸素と反応させてできる酸化銅は、

 

　A. (1) 12.5g

 

ということになります。

 

 

-----

それでは (2) に行きましょう！

この問題は、表のデータを使うのと、問題文の中の「銅と酸素は原子数の比が 1:1 で結びつく」ということを合わせて考えれば解を求めることができます。

 

Let's think!

 

(2) の問題。

「銅と酸素の質量比」と「銅原子１個と酸素原子１個の質量比」というのはきっちり分けて考えないといけません。この問題の場合は「銅と酸素は原子数の比が 1:1 で結びつく」ということなので、どちらの質量比も同じになるのですが、それもきっちり理解しておきましょう。

 

まずは「銅と酸素の質量比」について、表のデータから考えます。

 

銅 0.4g を酸素と完全に反応させてできるのが 0.5g の酸化銅です。ということは、

 

　0.5 - 0.4 = 0.1

 

銅 0.4g に対して反応した酸素の質量は 0.1g であることが分かります。そこから銅と酸素の質量比は、

 

　銅：酸素 = 4：1

 

となります。ここから「銅原子１個と酸素原子１個の質量比」を考えます。

 

「銅と酸素は原子数の比が 1:1 で結びつく」ということは、銅と酸素の原子の数はイコールになるということ。

 

これはつまり、「銅 0.4g、酸素 0.1g」があったとして、銅の原子数が仮に 100個だとしたら、酸素の原子数も 100個だということ。銅と酸素の質量をそれぞれの原子数で割ると原子１個あたりの質量が分かりますが、

 

　0.4 ÷ 100 = 0.004　←銅原子１個あたりの質量（仮）

　0.1 ÷ 100 = 0.001　←酸素原子１個あたりの質量（仮）

 

　銅原子１個の質量：酸素原子１個の質量 = 0.004：0.001 = 4：1

 

というように、原子数の比が 1：1 なら、「銅と酸素の質量比」と「原子１個ずつの質量比」も変わらず同じになるということですね。

 

よって、「銅原子１個と酸素原子１個の質量比」は、

 

　A. (2) 4：1

 

となります。

 

-----

ここからは仮定の話。

 

もしも、銅と酸素の原子が 1：3 とかで結びつくとしたら？を少しだけ考えてみます。

 

・「銅原子１個と酸素原子１個の質量比」が 4：1 の場合。

　銅と酸素の原子が 1：3 で結びつく、つまり 4：1+1+1 となるので

　「銅と酸素の質量比」は 4：3 となる

 

・「銅と酸素の質量比」が 4：1 の場合。

　銅と酸素の原子が 1：3 で結びついている、つまり 4：1/3 + 1/3 + 1/3 となるので

　「銅原子１個と酸素原子１個の質量比」は 4：1/3 = 12：1 となる

 

この理屈が分かるでしょうか。

これがきちんと分かっていれば (6) も解くことができますよ！

 

 

-----

それでは (3) に行きましょう！

この問題は、先ほどの問題を解く過程で得た、銅と酸素の質量比、から簡単に解くことができますね。

 

Let's think!

 

 

 

(3) の問題。

先ほどの問題で、銅と酸素の質量比は、

 

　銅：酸素 = 4：1

 

であることが分かっていますね。これを使って 6.0g の銅に反応する酸素の質量を求めます。

 

　4：1 = 6.0：x

　4x = 6.0

　x = 1.5

 

6.0g の銅に対し反応する酸素の質量は 1.5g であることが分かります。酸素は 6.0g あるとのことですが反応に使われた酸素は 1.5g だけなので 6.0 - 1.5 で、この問題の解は、

 

　A. (3) 酸素が 4.5g 残る

 

となります。

 

-----

それでは (4) に行きましょう！

この問題は、反応した酸素の質量、その質量の酸素で反応する銅の質量、を考えていけば解くことができます。

 

Let's think!

 

(4) の問題。

3.0g の銅粉を加熱しできた化合物の質量が 3.5g ということは 3.5 - 3.0 で 0.5g の酸素が反応したということが分かります。

 

　銅：酸素 = 4：1

 

から、酸素 0.5g と反応した銅の質量は、

 

　4：1 = x：0.5

　2.0 = x

 

3.0g のうち 2.0g の銅粉が反応したということなので、まだ反応していない銅の質量は

3.0g - 2.0g だから、

 

　A. (4) 1.0g

 

となります。

 

-----

それでは (5) に行きましょう！

この問題は、酸化銅の質量を求める、酸化マグネシウムの質量を求める、マグネシウムと酸素の質量比 3：2 からマグネシウムの質量を考える、という 3つのステップで考えてみてください。

 

Let's think!

 

(5) の問題。

銅粉にマグネシウムを混ぜて反応させた、ということだが銅粉は銅粉で分けて考えれば良い。

まずは銅粉 5.0g を完全に酸素と反応させたときの酸化銅の質量を考えます。

 

　銅：酸素 = 4：1

 

ここまで何度も使ってきた銅と酸素の質量比ですが、扱いやすいように少しパワーアップさせましょう。銅と酸素の比率が 4：1 ということは酸化銅の比率は 5 となりますね。

 

　銅：酸素：酸化銅 = 4：1：5

 

ここから、銅 5.0g に対する酸化銅の質量を求めます。銅 4 に対して酸化銅 5 なので、

 

　4：5 = 5.0：x

　4x = 25.0

　x = 6.25

 

銅粉 5.0g と反応してできた酸化銅は 6.25g であることが分かりました。

酸化銅と酸化マグネシウムの混合物の質量が 8.75g なので、ここから酸化銅の質量を引くと、

 

　8.75 - 6.25 = 2.5

 

酸化マグネシウムの質量が 2.5g であることが分かりますね。

問題文に「マグネシウムと酸素の質量比は 3：2」であると書いているので、ここから酸化マグネシウムの比率も考えて整理すると、

 

　マグネシウム：酸素：酸化マグネシウム = 3：2：5

 

マグネシウムと酸化マグネシウムの比率が 3：5 なので、

 

　3：5 = x：2.5

　7.5 = 5x

　1.5 = x

 

よって銅粉と混ぜたマグネシウムの質量は、

 

　A. (5) 1.5g

 

となります。

 

-----

それでは (6) - ① やってみましょう！

この問題は、酸化銅 22.5g と反応した酸素の質量を求めて考えれば良いですね。

 

Let's think!

 

(6) - ① の問題。

酸化物 Y 中の金属 X と酸素の比率を求めよ。で、まず分かっているのが酸化物 Y の質量が 15g だということ。

あとは問題文の中に「酸化銅 22.5g に含まれる酸素と同じ質量の酸素」と反応させた、と記載があるので、酸化銅 22.5g に含まれる酸素の質量を求めればいいですね。

 

　銅：酸素：酸化銅 = 4：1：5

 

酸素と酸化銅の比率は 1：5 なので、

 

　1：5 = x：22.5

　22.5 = 5x

　4.5 = x

 

酸化物 Y の質量 15g のうち、酸素の質量が 4.5g なので、金属 X の質量は、

 

　15 - 4.5 = 10.5

 

となる。あとは金属 X と酸素の質量比を求めればいいので、

 

　10.5：4.5 = 105：45 = 7：3

 

よって答えは、

 

 

　A. (6) - ① 7：3

 

となります。

 

-----

それでは (6) - ② やってみましょう！

この問題は、(2) の問題の解と、問題文にある「銅原子と金属 X の原子の質量比」とを合わせて考えてみましょう。

 

Let's think!

 

(6) - ② の問題。

問題文に「銅原子１個と金属 X の原子１個の質量比」が「8：7」であると書いてありますね。あとは (2) のところで「銅原子１個と酸素原子１個の質量比」が「4：1」であることも分かっています。

 

この二つの比率の共通項である「銅原子１個の比率」を揃えてあげれば、金属 X と酸素の原子１個の質量比を求めることができますね。

 

　銅原子１個：金属 X の原子１個 = 8：7

　銅原子１個：酸素原子１個 = 4：1 = 8：2

 

銅と酸素の比率を 2倍にして調整してあげると、銅の比率を揃えることができます。

 

銅原子の比率「8」に対して、金属 X の原子の比率が「7」

銅原子の比率「8」に対して、酸素原子の比率が「2」

なのだから、

 

　金属 X の原子１個：酸素原子１個 = 7：2

 

と考えることができますね。よって答えは、

 

　A. (6) - ② 7：2

 

となります。

 

-----

それでは (6) - ② やってみましょう！

この問題は、① の比率と ② の比率が異なるという点がポイントです。物質の質量比と、その物質の原子１個の質量比が異なる、ということは原子同士が結びつく個数の比が 1：1 ではないということ。それを踏まえて考えてみてください。

 

Let's think!

 

(6) - ③ の問題。

①と②の問題の答えから、

 

　金属 X ：酸素 = 7：3

　金属 X の原子１個：酸素原子１個 = 7：2

 

であることが分かっています。原子の質量比と物質の質量比が異なるということは、結びつく原子の個数が異なるということ。

 

原子の比率 7：2 で、原子の数がいくつといくつで結びつくと物質としての質量比が 7：3 になるのか、を考えれば良いですね。

 

少し考えやすいように原子の方の比率を少し変形させます。

 

　金属 X の原子１個：酸素原子１個 = 7：2 = 3.5：1

 

これを物質の質量比 7：3 になるようにすると、

 

　金属 X の原子２個：酸素原子３個 = 3.5 + 3.5：1 + 1 + 1 = 7：3

 

よって金属 X と酸素の原子数の比は

 

　A. (6) - ③ 2：3

 

となります。

 

-----

最後の問題の金属 X ですが、質問をくれた生徒は授業のあとにその正体を友達と一緒に調べてみたそうです。

 

答えは「鉄」だそう。

 

酸化鉄の化学式を調べてみると、

 

　酸化鉄(II)、酸化第一鉄：FeO

　酸化鉄(III)、酸化第二鉄：Fe₂O₃

　酸化鉄(III)鉄(II)、四酸化三鉄：Fe₃O₄

 

など、さまざまな種類があるようですね。この問題の酸化物 Y というのは酸化鉄(III)ということになるのかな。

中学の勉強の範囲からは逸脱するけれど、興味がある人は調べてみると面白いかもしれないですね。

 

 

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

 
ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 

以上です。お疲れさまでした！

(*ᴗˬᴗ)⁾⁾

 

生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、とある中学の「2年 1学期 中間テスト」で出題された、理科(1年 地学) の問題です。

 

 

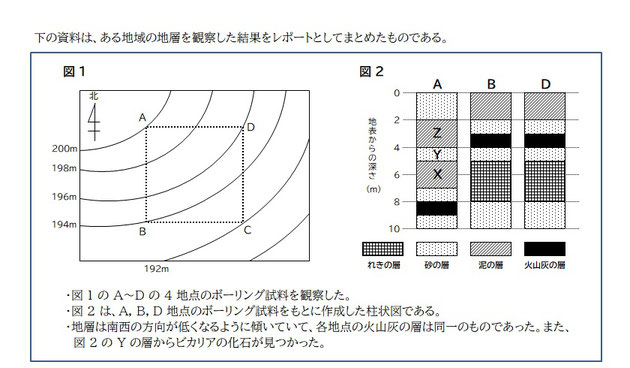
今回は理科の問題。柱状図の読み取りが苦手、というか全然分かってない、っていう子は多いのではないでしょうか。

 

実はそんなに難しいことではないのでしっかり見直ししていきましょう！とりあえず柱状図の前に、まずは知識を問う設問 (1) と (2) から！

 

Let's think!

 

まずは化石についてのおさらい。化石には 2 種類ありましたね。

 

　示相化石 ･･･ 地層ができた当時の「環境」を推定する手がかりとなる化石。

　　　・サンゴ（あたたかくて浅い海）

　　　・ブナ（寒冷な気候）

 

　示準化石 ･･･ 地層ができた「時代」を推定する手がかりとなる化石。

　　　・古生代：フズリナ、三葉虫

　　　・中生代：アンモナイト、恐竜

　　　・新生代：ビカリア、マンモス

 

 

ざっくりまとめるとこんな感じでしょうか。これだけ押さえていれば (1) と (2) は簡単に正解することができますね。

 

　A.　(1) 示準化石　　(2) 新生代

 

 

(3) は堆積についてちゃんと分っていないと解くのは難しいですね。当てずっぽうで正解しても意味がないです。答えが何か、が分かっただけでも意味がないです。答えが分かったら、どうしてその答えになるのか、について理解できるまで見直しましょう。

 

Let's think!

 

さて、(3) です。柱状図を見ると、

 

「X」泥の層、「Y」砂の層、「Z」泥の層、

 

となっていますね。ここから何を読み取ればいいのか。地層がどのように形成されるのか、見ていきましょう。

 

　Step1.  風化：気温の変化・太陽光・氷結・風雨などの影響で、岩石がもろくなる。

　Step2.  浸食：雨水や流水によって岩石が削られ土砂となる。

　Step3.  運搬：流水によって土砂が運ばれる。

　Step4.  堆積：運ばれた土砂（れき、砂、泥）がたまり積み重なっていく。

 

　堆積の仕方

　　粒の大きなもの：流されにくいため、海岸から近く浅い水底に堆積していく。

　　粒の小さなもの：流されやすいため、海岸から遠く深い水底に堆積していく。

　　粒の大きさ：　(大) ←　れき　砂　泥　→ (小)

 

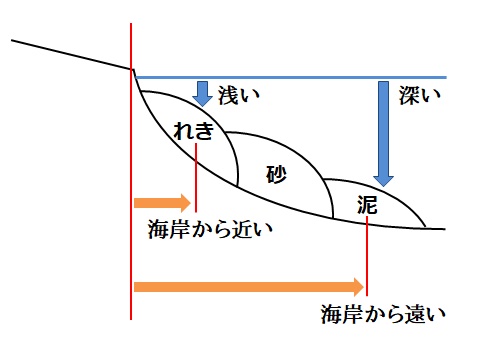
つまり、地層の種類から、

 

　「れきの層」が形成された

　　　→以前の層（下のある層）が、

　　　　「砂」「泥」のいずれでも、地面の位置が「高い」場所に移動した（隆起）

 

　「砂の層」が形成された

　　　→以前の層が、

　　　　「れき」なら、地面の位置が「低い」場所に移動した（沈降）

　　　　「泥」なら、地面の位置が「高い」場所に移動した（隆起）

 

　「泥の層」が形成された

　　　→以前の層が、

　　　　「れき」「砂」のいずれでも、地面の位置が「低い」場所に移動した（沈降）

 

というようなことを読み取ることができるというわけです。

 

 

さて、では (3) を見ていきます。ここまできちんと理解していれば解くのは簡単ですね。

 

地層は古い時代のものから、

 

　「X」泥の層　→　「Y」砂の層　→　「Z」泥の層

 

の順で形成されているので、

 

　「X」泥の層が形成される、深い場所にあった

　「Y」高い場所に移動し（隆起）、砂の層が形成される

　「Z」深い場所に戻り（沈降）、泥の層が形成される

 

地層の形成順序によって以上のように読み解くことができますね。よって答えは、

 

　A.　(3) ウ 【隆起してから沈降した】

 

 

 

次の問題は柱状図の読み取りです。柱状図の位置をきちんと揃えて並べてあげる、のがポイントですね。

 

Let's think!

 

では (4) を見ていきましょう。

 

柱状図を見るときに気を付けなければいけないことは、柱状図は全て地表 0 メートルを基準にして揃えられ書かれている」ということです。

 

図 2 の柱状図、きれいに並べてありますが、図 1 を見ると各地点の地表 0 メートルの標高はバラバラであることが分かりますよね。

 

ですので柱状図を見るときは、

 

　柱状図の「地表 0 メートル」を、各地点の標高の位置に合わせること

 

が大切なポイントとなります。地表 0 メートルで揃えられた柱状図を、各地点の標高ごとに並べなおします。

 

問題の 図1 を見ると標高は、A地点：200ｍ、Ｂ地点：194ｍ、D地点196ｍ、です。

それぞれの標高に、柱状図の地表 0m を並べなおすと ↓ のようになりますね。

 

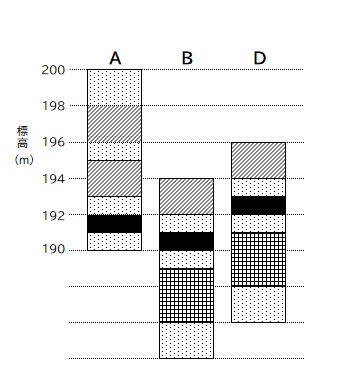
この並べ替えさえできてしまえば、あとはこの図から回答となる情報を読み取るだけ。

 

　A.　(4)　① 1　　②192　　③193

 

 

さぁ、次で最後の問題です。

 

Let's think!

 

(5) は C 地点の火山灰の層の位置を推察する問題ですね。

 

そのために必要な情報は「地層は南西に傾いている」という点。(4) の問題文の中になる情報を整理し、C 地点と比較をすると。

 

　地層は南が低くなる：A より B が 1m 低い

　　　　　　　　　　　→ C より北にある D と比較すると、D より C が 1m 低い

 

　地層は西が低くなる：D より A が 1m 低い

　　　　　　　　　　　→ C より西にある B と比較すると、C より B が 1m 低い

 

となる。解を求めるには上記のどちらを利用しても構いません。

図に書いて比較してみよう。

 

　↑↑↑

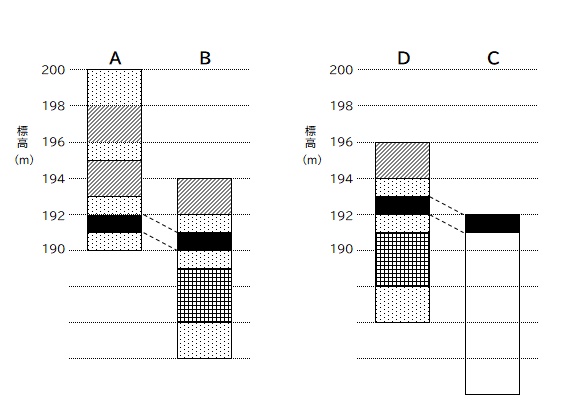
A 地点と B 地点の火山灰層の高低差をもとに、

　　　D 地点から C 地点の火山灰層の位置を推測する。

 

　↑↑↑

A 地点と D 地点の火山灰層の高低差をもとに、

　　　B 地点から C 地点の火山灰層の位置を推測する。

 

 

いずれの方法でも C 地点の火山灰層の位置は同じになりますね。

 

　A.　(5) C 地点の火山灰の層は 0～1m の位置　※回答は上記図の通り

 

 

-----

 

今回も記事を書くのにそれなりに時間をかけ、たくさんのことを調べました。だからこそ、その過程で得た知識が身についていくのです。

 

知りたいことのために時間をかけること、その中で新たに生まれた「気になること」も時間をかけて調べること。寄り道こそが知識の量と幅を広げる最短の道だったりします。

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾