生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。

 

 

この問題は、「２つの連立方程式の解は同じ」、これの意味をきちんと理解できるかどうか、がポイントかな。そこさえ分かれば、あとは、

 

1. 連立方程式を解き x , y を求める。

2. x , y を代入、方程式を解き a を求める。

3. x , y を代入、方程式を解き b を求める。

 

これだけなので簡単ですね。では解いていきます。

 

 

まずは「２つの連立方程式の解は同じ」ということについて。解が同じになるということは、４つの方程式のうち、連立方程式をどの組み合わせで解いても x , y の値が同じになるということ。

 

連立方程式の勉強をしている時点では、次の単元である一次関数は当然習っていないのだけれど、「２つの連立方程式の解は同じ」ということがどういうことかを簡単に理解するために一次関数のグラフで考えてみます。

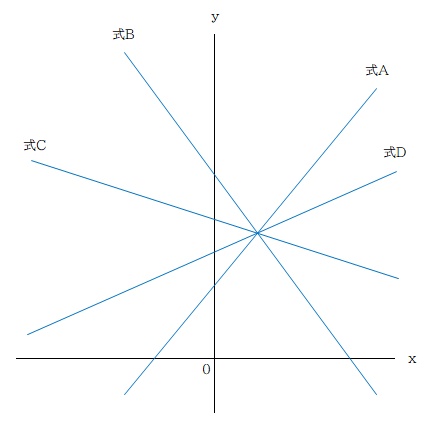
グラフにするとこんなイメージかな。

 

　すべての解は同じ → x , y が同じ → すべての式 (直線) の交点が同じ

 

っていう感じ。どの式の組み合わせで連立方程式を解いても良いということになります。

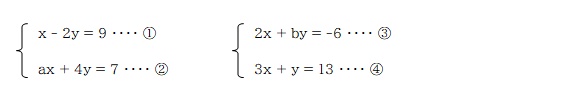
ひとつの方程式のなかに文字 (分からない値) が３つ含まれている式②③は使えないので、式①④を連立方程式で解けば良い、ということですね。

 

ここさえ理解できればあとはただの計算問題です。

 

　x - 2y = 9 ･･･ ①

　3x + y = 13 ･･･ ④

 

①を 3倍して、

 

　3x - 6y = 27 ･･･ ①´

 

①´から④を引く

 

　3x - 6y = 27

　3x + y = 13

 

　-7y = 14

　y = -2

 

y の値を①に代入

 

　x - 2y = 9

　x + 4 = 9

　x = 5

 

x=5 , y=-2 を式②③に代入し a , b を求める

 

　ax + 4y = 7

　5a - 8 = 7

　5a = 15

　a = 3

 

　2x + by = -6

　10 - 2b = -6

　-2b = -16

　b = 8

 

A. a=3 , b=8

 

 

この問題は、最初に式①②と式③④がセットで提示されているので、「解が同じ」の意味をちゃんと考えられないと、「式②③で連立方程式で解けばいいんだ！」という発想に至らないのかもしれないですね。

 

一次方程式も連立方程式も、他のどんな単元の文章問題もすべて同じですが、問題を解くために必要な情報は全て問題文の中に用意されています。

 

大切なのは与えられた情報をちゃんと読み解くこと。

 

 

ちなみに勉強ができない子は「問題文を読んで考える」のではなく「問題文を見て解き方を知ってる問題かどうかを判断している」だけのことが多い。

 

なので、そういう子の「先生、この問題分かりません」という質問は「先生、この問題の解き方を知りません」ということが大半です。

 

 

文章問題を解けるようになりたいなら、まずは問題文をちゃんと読んで考えること！

勉強頑張ってくださいね！

 

 

----

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってください。

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾