生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学(式の計算) の問題です。
問題
次の計算をしなさい。

これだけ?そうです。たったこれだけの基本的な計算問題です。
けれど、子どもたちがよく間違えるポイントがふたつもあるので、その点も踏まえてみていきたいと思います。
-----
◆間違いやすいポイント、その1:方程式の計算と混同している。

このように、12 をかけて分数の分母を処理しようとして間違うパターン。これは方程式の勉強をしてきた中学2年生の子がよくやる間違い。
方程式の場合は「両辺に同じ数をかける」から左辺と右辺のイコールの関係が崩れず成り立つのであって、文字式の場合はこのまま計算しただけでは正解することはできないです。

式に 12 をかける、ということは、イコールの向こう側にある「この計算の解」も 12倍されることになるからですね。そのことをきちんと理解していればこの方法で解くことも可能です。それは後ほど。
-----
◆間違いやすいポイント、その2:符号ミス。

マイナスの分数で分子が多項式になっているとき、その多項式中の + や - の符号ミスが多いです。これは文字式でも方程式でも同じ。
計算の仕方をきちんと理解していないと本当によく間違うポイントのひとつですね。
では、解いていきます。
この計算式は方程式ではないので、基本の解き方としては通分して分母を揃え計算を進めていきます。
通分した後、x の項と y の項をそれぞれ計算するため、
「12 分の 2x-8y」を
「12 分の 2x」と「12 分の 8y」に分けるときの符号に注意です。
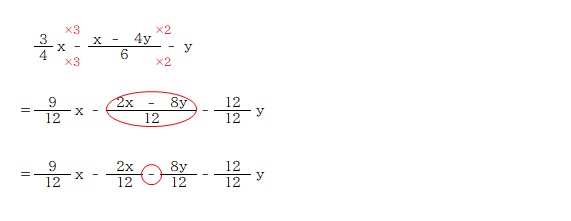
このように「マイナス」にしてしまうのは不正解です。
この計算は「2x から 8y を引いたものを前の数から引いている」のであって、「2x と 8y 両方を前の数から引いている」のではないからですね。
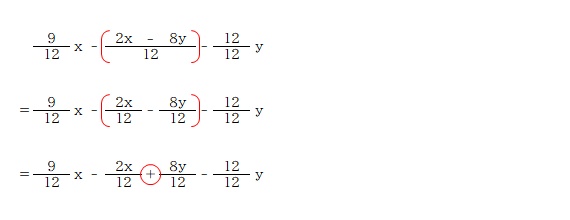
このように括弧を書いて計算すると間違いにくくなると思います。
あとは普通に計算するだけ。

次は、方程式のように分母を処理する方法での計算について。

この計算方法でも同じようにこの部分で符号ミスが多いです。なので先ほどの通武運の計算のとき同様、括弧を付けて考えると間違いにくくなります。
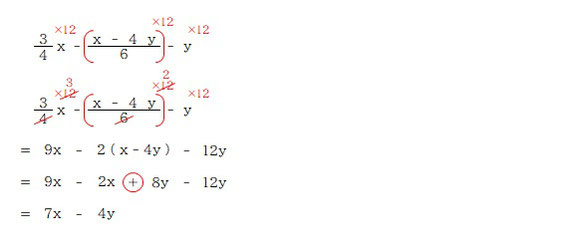
このように符号は + が正解。間違えないように気を付けましょう。
そして最後に、この計算方法は式を 12倍しています。ということは、そこから求められた答えも 12倍されているということ。
つまりここでの解「7x-4y」は本来の答えを 12倍したもの、ということになります。
言い換えると「7x-4y」を 12分の 1 にすれば本来の解になるということ。

一つひとつの計算の意味をきちんと理解していれば、どちらの解き方でも問題なく解くことができます。
しっかり理解して自由自在に扱えるように勉強頑張ってください!
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾








コメントをお書きください