生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

今回は、塾にあるワークからの出題、数学(2年 連立方程式) の問題です。

今回は、昨日の記事（「分からない」を考えよう！ #9）で解いた問題と同じ、割合の計算を含む連立方程式の文章問題です。

なので、昨日の記事を読んでしっかりと勉強をした子なら簡単に解ける問題！

そのはず、なんだけど。

解くことはできる、なのに、正解できない。

そんなトラップが仕掛けられた問題です。ホントはトラップなんていう大層なものではないのだけれど、「昨日の問題を解いている」ということで引っかかる子、気づけない子は多いです。

正解を出せるかどうか、ぜひチャレンジしてみてください。

Let's think!

去年の男子と女子の数が分からないので x , y として考えます。

男子は去年 x人いて、今年はそこから 10%減った、

つまり去年を 100%としたとき今年は 90%になった。なので 0.9 を掛ければいい。

女子は去年 y人いて、今年はそこから 4%増えた、

つまり去年を 100%としたとき今年は 106%になった。なので 1.06 を掛ければいい。

合計は去年の人数から減った分を引けばいいですね。

男子と女子の和が合計なので、

これで２つ式ができたので、あとは連立方程式で解けばいいですね。

-----

②の式に 100を掛けて小数をなくす。

①の式に 90を掛けて、x の項を②´の式と揃える。

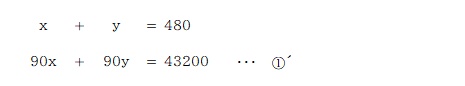
②´の式から①´の式を引いて y を求める。

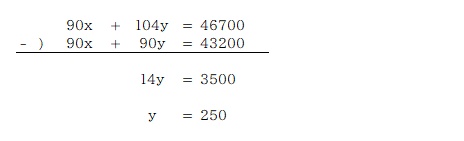
①の式に y の値を代入、x を求める。

ということで、

男子の人数 230人、女子の人数 250人

なのですが！

これが答えだと思った子は残念ながら不正解です。

なぜでしょう。たてた式は正しいです。計算も間違っていません。x と y の値も間違っていません。けど正解ではありません。

なんでなのか？考えてみてください。

Let's think!

なんで正解にならないのか、分かりましたか？

不正解を言い渡し見直しをさせると、生徒は必ずノートを見直します。式が間違っていないか、計算が間違っていないか、けどどちらも間違っていません。

なかなか不正解になった理由に気付けません。

それもそのはず。見直すべきは式や計算といった問題を解く過程ではないからですね。そもそもの前提が間違っています。

なので見直すべきは「問題文」です。

よく読んでみましょう。最後の一文です。

　「今年の男子、女子それぞれの生徒数を求めよ。」

求めるのは去年の人数ではなく、今年の人数なんですね。なのでこの解き方で x , y を求めるだけだと不正解になってしまうのです。

とても簡単なことですが、この手の問題を解いたことがあって、表面的な問題の解き方だけを覚える勉強に慣れてしまっている子、なんかはホントによく引っ掛かります。

ということで、この問題の解を求めるには連立方程式で解いた x , y の値を、今年の人数である、男子：0.9x と、女子：1.04y に代入して解としないといけないというわけ。

今年の男子の人数：

0.9x = 0.9×230 = 207人

今年の女子の人数：

1.04y = 1.04×250 = 260人

　A. 今年の男子：207人、女子：260人

となります。

-----

ちなみに連立方程式の解がそのまま正解にならないのは、「去年の人数を x , y 」としているからです。

なので「今年の人数を x , y」として解けば、その解がそのままこたえになりますね。

せっかくなので考えてみてください。

難しいポイントは、10%減った/4%増えた、というのが「去年の人数」の対する割合だということ。そこの計算をどうするかですね。

ヒントは税込みの値段を、税込み前の元の値段に戻す計算、を考えればいいですね。

Let's think!

今年の人数を x , y としたとき、去年の人数を x , y を使った数式で表さないといけません。

よくある間違いで、

　去年→今年：10%減った、今年→去年：10%増やせばいい

　去年→今年：4%増えた、今年→去年：4%減らせばいい

と考えてしまう子もいたりしますが、

10%減った/4%増えた、というのはあくまで「去年の人数」の対する割合なので、これでは不正解。

考え方は、

　男子の人数は、去年を 100% としたとき、今年は 90% なのだから、

　　今年を 90% と考え、それを 100% に戻せば去年の人数になる。

　女子の人数は、去年を 100% としたとき、今年は 104% なのだから、

　　今年を 104% と考え、それを 100% に戻せば去年の人数になる。

という感じ。

もっとシンプルに考えるなら、

　たとえば、5倍した数を元の数に戻したいなら？

　→5 で割ればいいよね。

というだけの話。

つまり、

　男子、去年の人数に 0.9 を掛けたのが今年の人数、ということは

　　→今年の人数を 0.9 で割れば去年の人数になる。

　女子、去年の人数に 1.04 を掛けたのが今年の人数、ということは

　　→今年の人数を 1.04 で割れば去年の人数になる。

なので、式にするとこんな感じ。割合の考え方、その計算、しっかりと理解して使いこなせるようにしておきましょうね。

あとは、計算していくだけ。

ただ計算は、去年を x , y としたときよりも少しめんどくさくなります。

-----

まずは③の式を連立方程式で解きやすい形に変形していきます。

④の式に 90を掛けて、x の項を③´の式と揃える。

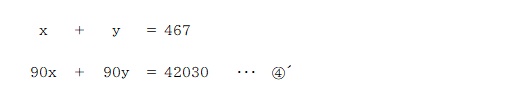
③´の式から④´の式を引いて y を求める。

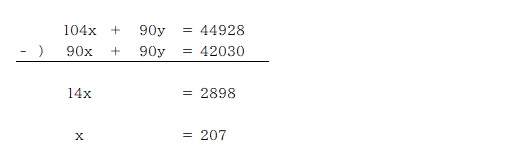
④の式に y の値を代入、x を求める。

先ほどの正解と同じ解を得ることができましたね。

問題の解き方はひとつではありません。

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾