生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。

 

 

 

この問題は、連立方程式の章の中で出題されていた問題です。問題の中にある「解が無数にある」と「解なし」を理解するのにどうすればいいかを色々と考えていました。

 

多分、それを理解しようとするなら一次関数のグラフに式の線を書いて考えるのが分かりやすいのではないか、と思うのですが、この問題が出題された時点では当然まだ一次関数を学んではいないので、「解・無数」と「解・なし」を理解するのはなかなか難しいかもしれませんね。

 

まぁ、それは一旦置いておいて、まずはチャレンジ！

 

Let's think!

 

さて、どういうふうに進めるか。

いろいろ考えたのだけれど、とりあえず解答・解説を見てみましょうか。

 

 

この解説を読んで理解できるかどうか、です。

 

問題を解くときに「解答を見る」というのはダメなこと、悪いこと、そういうイメージがあるかもしれないですが、きちんと理解するためのアプローチとしては「解答を見る」のは全然アリです。

 

「解答を見る」ことがダメなのではなく、

 

「解答を見て、答えを写して終わらせる」ことがダメなのです。

 

解答を見てからが勉強です。

解答を見て、問題を解く考え方を理解しようする努力をしているかどうか。

 

勉強ができる子と、できない子の差が付くポイントのひとつです。

勉強ができる側に立ちたい！と思うのならぜひ実践してください。

 

 

 

さて、言いたいこと言うのに話が逸れましたね。

 

正直私はこの解説を読んできちんと理解できる子は、あんまりいないんじゃないかなぁ、と思います。

 

けれど、とりあえずは考えてみてください。

 

Let's think!

 

それでは、連立方程式の「解・無数」と「解・なし」について、どういうことなのか。どう理解すればいいのか、考えていきましょう。

 

少しズルい気もしますが、連立方程式の勉強をしている時点ではまだ勉強していない一次関数の知識を使って解説していきたいと思います。

 

なので、この記事を読んでいる時点で「まだ一次関数の勉強をしていない」子は、一次関数の勉強をしてから読み直してみると分かりやすいかもしれません。

 

 

-----

一次関数では、

 

　y = ax + b

 

という形で式を扱います。１年生のときに勉強した比例の式は「y = ax」でしたね。比例の式が原点 (0,0) を通るのに対し、一次関数の式は原点を通りません。

 

　ａ：傾き

　式をグラフに示したときの直線の、文字通り傾きを表しています。

 

　ｂ：切片

　式をグラフに示したときの直線の y軸との交点、y軸上の y座標を表しています。

 

　y軸→つまり x座標が 0 です。一次関数の式に x=0 を代入すると、

 

　　y = a × 0 + b

　　y = b

 

　座標が (0,b) となり、切片 b が y軸上の y座標であることが分かりますね。

 

 

実際にグラフに書いてみます。

 

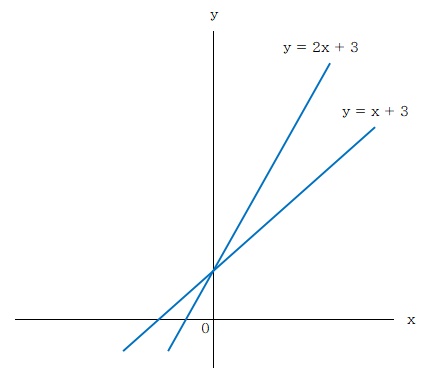
傾き a の値が変われば、直線の傾斜が変わります。

 

 

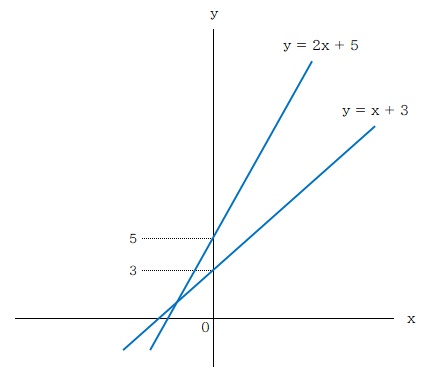
切片 b の値が変われば、y軸との交点の位置が変わります。

 

 

 

 

ザックリとですがここまでが、一次関数の式とそれをグラフに示したときの直線について、の説明です。

 

 

 

 

では、ここからは連立方程式の「解・１つ」「解・無数」「解・なし」というがどういうことかを一次関数のグラフに書いて説明します。

 

 

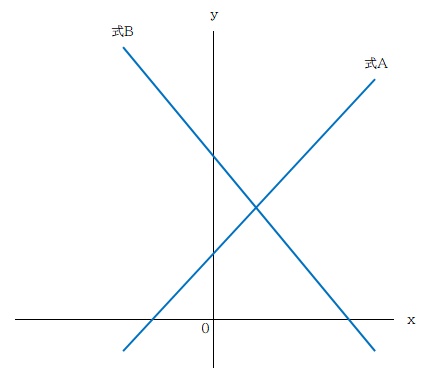
「解・１つ」

連立方程式の解は、ふたつの直線の交点の x座標と y座標を表しています。

 

一次関数の式の形にしたとき、傾き a の値が異なります。

同じにはなりません。

同じになる場合、というのが次に示す「解・無数」「解・なし」のケースになります。

 

 

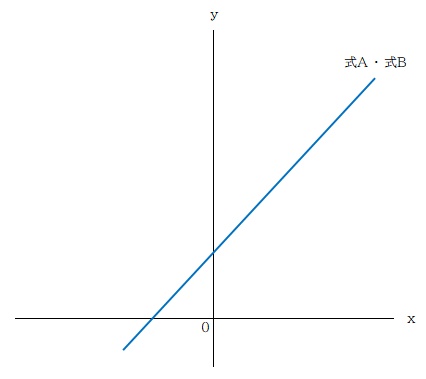
「解・無数」

連立方程式の解は「ふたつの直線の交点」ということでしたね。このようにふたつの直線が完全に重なる場合、ふたつの直線のすべてが交点となり、連立方程式の解が無数にある、ということになります。

 

一次関数の式の形にしたとき、傾き a の値と切片 b の値がどちらも全く同じ式、ということになりますね。

 

 

「解・なし」

連立方程式の解は「ふたつの直線の交点」ですが、このようにふたつの直線が平行になる場合、平行な２直線は決して交わることがないので解がない、ということになります。

 

一次関数の式の形にしたとき、傾き a の値が等しく、切片 b の値が異なる式、ということになりますね。

 

 

 

どうでしょうか。連立方程式の解について、グラフで示すと「なるほど！」ってなりませんか。多分、分かりやすいと思うのです。

 

では、ここまで学んだ内容を踏まえこの問題の解を考えてみてください。

 

Let's think!

 

それでは問題を解いていきます。

 

まずはふたつの式を一次関数 y=ax+b の形に直してみましょう。

 

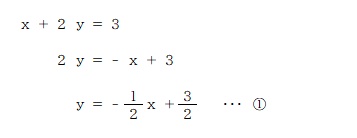
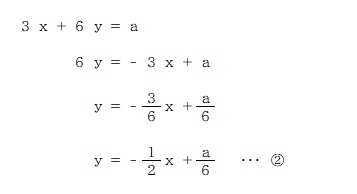
このようになりますね。

 

まずは、解が無数にある、とはつまり①と②の直線がぴったりと重なる状態ということでした。

 

傾きは①と②どちらの式も同じす。なので切片が等しくなるような値を考えれば良いですね。

 

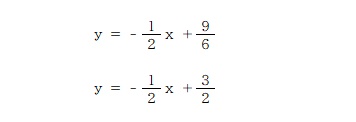
②の式に a=9 を代入してあげると①と同じ式が出来上がります。

 

よって「解が無数にある」のは a の値が 9 になるとき、ということになります。

 

 

そして、解がない、というのは①と②のふたつの直線が平行に並ぶ場合。つまり切片の値が同じにならなければ良いということ。

 

　a=9 で①と②の式の切片の値が同じになる

　　↓

　a=9 以外の値であれば①と②の式の切片の値は同じにならない

 

よって「解がない」のは a の値が 9 以外になるとき、ということになります。

 

 

　A. (解が無数にある) a=9 のとき、(解が１つもない) a=9 以外の値をとるとき

 

 

 

いかがでしたか？

 

この記事を読んで、連立方程式の解が無数にある、解がひとつもない、ということがどういうことか理解できた！という子がひとりでもいてくれたらうれしく思います！

 

 

-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾