生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。
問題

なかなか難問ですね。解き方を知らない問題はワクワクします。解き方を知っていればただの作業ですからね。
それではチャレンジしていきましょう!ご覧の皆様もまずは考えてみてください。
Let's think!
問題文を読んで、書いてあることを正しく理解するだけでも難しい、と感じる子もいるかもしれないですね。
(1) は問題にある [ ] で挟んだ数字が何を意味するのか、問題文を読んでちゃんと理解できたかどうかを確認する問題、といったところでしょうか。
問題として出されているのは [10213] なので、この値を求めるには 10213 を 7 で割ったときの余りを求めればよい、ということになります。
10213 ÷ 7 = 1459 … 0
割り切れましたね。よってこの問題の解は、
A. 0
となります。さて、ここまでは問題の意味が理解できたか、の確認作業。いわば前座のようなもの。次の問題が本番ですよ!
Let's think!
さて、(2) ですが、私の場合はとりあえず数字の小さいものからいくつか計算してみることにしました。2~5乗くらいまでなら計算にさほど時間もかからないと思います。
頭の中だけで考え込むより、考えたことはすぐに手を動かしアウトプットする。トライ&エラーの繰り返しの中から問題を解くためのヒントを見つけ出します。

5乗まで計算してみて、あることに気付きます。余りが 1, 6, 1, 6 と繰り返していますね。これは大きなヒントになる気がしました。
もちろん、たまたまここまでは繰り返しになっているが 6乗の余りは違う数字になるかもしれません。
ですので、今度はこの「余りの 1 と 6 が繰り返していく」という法則が正しいことの証明について考えていく必要がありますね。
その方法の一つに、6乗、7乗、8乗とすべて計算して力ずくで解を見つける、という手段もあるといえばありますが、私はそこまで大きな数の計算はしたくないのでやりません。
というわけで、続きを考えてみてください。
Let's think!
まず、(6の2乗) の余りは 1 です。
これはつまり「(6の2乗)-1」は 7の倍数である、というように言い換えることができます。
(6の2乗)-1
→7の倍数である。7 で割ると 1 余る、ということを表している。
これを元に考えていきます。
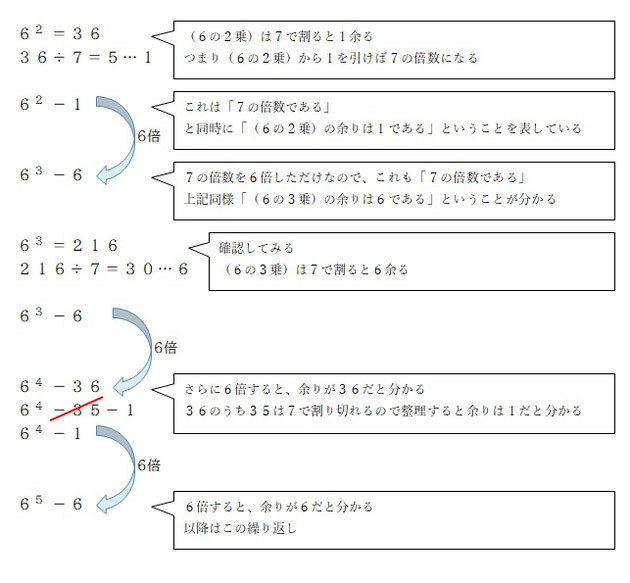
私の場合は、こんな感じで考えをまとめました。
これで、6 の偶数乗の余りは「1」、6 の奇数乗の余りは「6」、であることが証明できたと思います。
よって、6 の x乗のうち、余りが 1 となる 2桁で最小のもの、その解は、
A. x=10
となります。
さて、私なりに考えて、私なりの解き方を書かせていただきましたが、実際どうなんでしょうね。この問題を作られた先生の解説を聞いてみたいです。
もっとシンプルな考え方があるのかもしれません。
これだけのことを考え整理するのにもそれなりの時間がかかりますから、たとえば推測と力技の組み合わせで、
1. 6 の 2~5乗を計算、7で割って余りを求める
2. 余りが 1, 6, 1, 6 続くことから、10乗の余りが 1 になる可能性が高いのではないか、と仮説を立てる。
3. 仮説の実証のため 6 の 10乗を計算し 7 で割って余りを求める
4. 計算を間違えなければ余りは 1 となるので解が x=10 と求めることができる
という解き方でもいいのかもしれません。6 の 10乗の計算にどれだけ時間がかかるかは、やっていないので分かりませんが。
面白い問題だったので是非いろいろ考えてみてください。
ちなみにおまけ。エクセルを使った 6 の x乗の計算結果です。
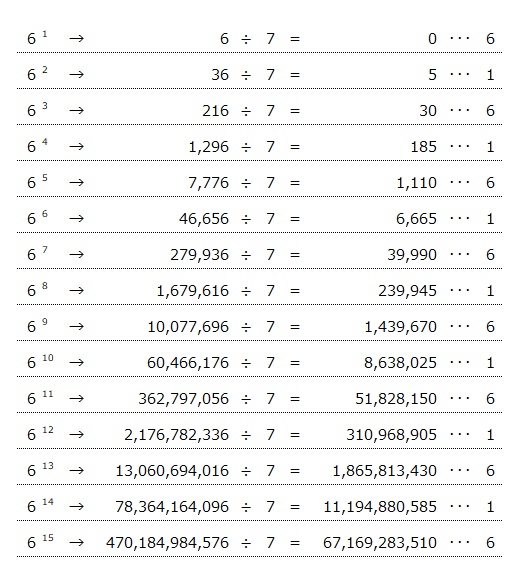
こういうもの簡単に作ることができます。エクセル、便利ですね。そして、こうして見ると 6 の 10乗くらいなら計算もそこまで苦にはならない気がしますね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾








コメントをお書きください