生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。


今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。

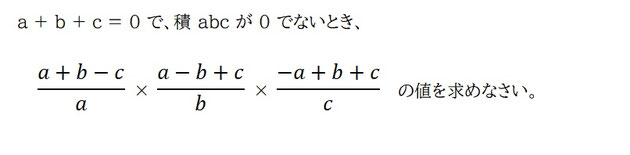
今回のテスト問題を見た中で個人的に「一番面白そう！」と思った問題です。ちなみに、その生徒のクラスで正解できたのは3人だけだったそうです。

さて、一番面白そう、と思った理由はパッと見て解き方が分からなかったから！

なのでワクワクしながら挑戦スタートです。

まず、解き方は分からない、が、上手いこと式を整理してあげれば良いんだろうな、ということは分かっていました。問題はどういう整理の仕方をするか、ですね。

こういうときは、

(1) とりあえずこの問題は飛ばして解ける問題を解いていく。

(2) とりあえずできる計算をやってみる。

その過程でこの問題を解くヒントが見つかるかもしれません。私はとりあえず、そのまま計算してみました。頭の中だけで考え込むより、まずは手を動かすのが性に合っています。

Let's think!

とりあえず計算してみたら、いろいろ打ち消しあっていい感じに整理されたら良いなー、と思いつつ、一方では多分これじゃ無理だろうなー、とも思いながら計算してみました。

計算しつつも、頭の中では式を整理するための工夫を考えながら。

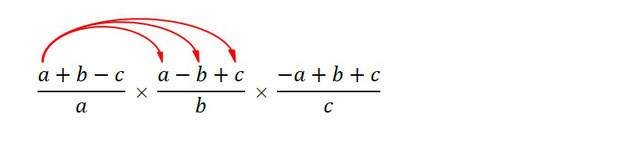
こんな感じで、本当にただ計算して整理してみます。

ここまで計算してみましたが、赤丸の同類項を整理してもこれ以上はどうにもならなそうですね。そもそもこの計算をするだけで時間がかかり過ぎていて、時間制限のあるテストの中ではこんなことをしている余裕はないでしょう。

正面突破は無理、ということが分かりました。

そこで問題文を最初から見直すと、そういえばもう一つ式あるよね、ということに気づきます。

a+b+c=0

実はこの式こそが問題を解くためのカギ！問題の式の中に a+b+c があれば 0 を代入することができます。ですが、問題の数式の分子の部分には、

a+b-c 、a-b+c 、-a+b+c

というように、どれもマイナスが入っていて代入することができません。マイナスの項が邪魔です。なので、ちょっと整理してみました。

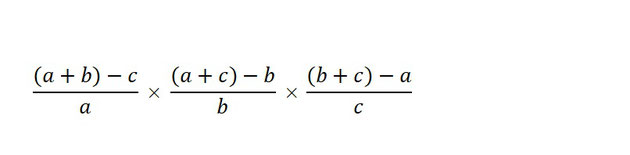
私の場合はここでピンときました。

a+b+c を代入できる個所は無い、けれど a+b だけなら代入できそうです。a+c 、b+c も同様です。

問題を解くためのカギ（a+b+c=0）はある。でもこのままでは問題のカギ穴には合わない。じゃあカギの形のほうを変えてしまえば。さて、それでは、

Let's think!

問題文にある a+b+c=0 を次のように変形させます。

　a + b = -c

　a + c = -b

　b + c = -a

この形であれば代入して計算していくことができますね。

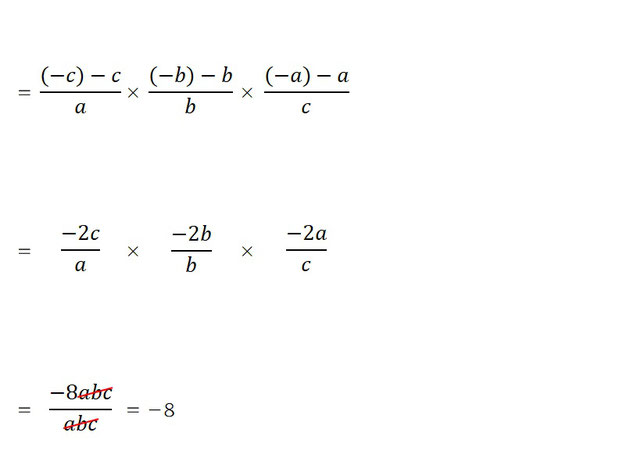
A. -8

キレイに整理され解くことができましたね。

-----

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾