生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。
【問題】

表の中の数字 N を、その数字の位置を表す座標 x,y の値から求める式を考えれば良いんだな、みたいなことをまず考えることができればいいですね。
そこでまずは数字の変化に規則性はないか、探してみましょう。
Let's think!
数字の変化の規則性、見つけることができましたか?
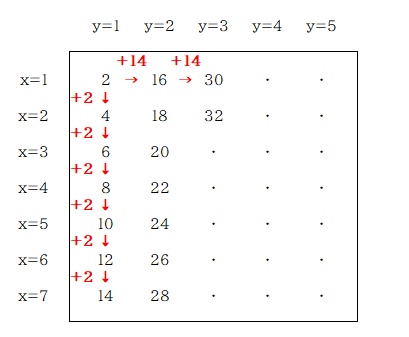
数字は偶数が順に並んだものなので 2 ずつ増えていきます。1つの列に 7つ並べたところで次の列に移ります。なので横の数字を見ると 14 ずつ増えているのが分かりますね。
では、この規則的な変化を x と y を使って表す数式を作っていきましょう。
Let's think!
まず縦方向の数式は簡単に思いつくと思います。

x=1 のときが 2 で、そこから x が 1 増えるごとに 2 ずつ増えていくので、シンプルに 2x という式が成立しますね。
ではさらに横の変化、y を絡めた式を作りましょう。

ヒントその1、です。
1行目だけを見て考えてみます。2、16、30、という数字を先に考えた 2x と合わせて作ることができればいい。1行目なので 2x に x=1 を代入し 2x=2 となります。
よって、横の数字を「x を使って求める数」と「y を使って求める数」に分けると、
2+0 、2+14 、2+28 と表すことができますね。
この 0 、14 、28 の部分を、y の値を使って求める式を作っていきます。
Let's think!
y を使った数式を作ることができましたか?できなかった人のためのヒントその2、です。

「2x+〇〇」の ○○ の部分を少し分解して考えてみます。
最初に変化の規則性を考えたときに、横の数字は 14 ずつ増えていると考えたのを思い出してみましょう。
14 の個数がいくつになるか、を考え、その個数を求める式を y の値を使って求める数式を考えるようにすると、すごく分かりやすくなったと思いませんか?
整理すると、
「2x+〇〇」の ○○ の部分を求める数式を考える
↓
「2x+(14×〇〇)」の ○○ の部分を求める数式を考える
ということになりますね。では、最後です。y の値を使って 〇〇 の部分を求める数式を作ってみましょう。
Let's think!
「2x+(14×〇〇)」の ○○ の部分、14 の個数を求める部分の数式は、
y=1 のとき 0 、y=2 のとき 1 、y=3 のとき 2
となる。つまり「y の値より 1 小さい数」ということが分かるので y-1 とすれば求めることができますね。
よって N を求めるための数式、その答えはこのようになります。
N = 2x + 14(y-1)
では、これが正しいか確認です。問題文にある N(3,2) を代入して解が 20 になるかどうか。他にも適当に N(5,2) とか N(1,3) とか試してその位置の値を求めることができれば ok ですね。
この数式さえ完成してしまえばあとは簡単。
(1) N(3,5) を代入して値を求める。
(2) x=1 を代入して式を整理する。
Let's think!
(1) N(3,5) を代入して値を求める。
N = 2x + 14(y-1)
N = 2×3 + 14(5-1)
N = 6 + 14×4
N = 6 + 56
N = 62
A. 62
-----
(2) x=1 を代入して式を整理する。
N = 2×1 + 14(y-1)
N = 2 + 14y - 14
N = 14y - 12
A. N = 14y - 12
ちなみに、この問題の答えの数式が何を表すものなのか?っていうのは分かりますか?
この式は「1行目限定で y 列目の値を求める数式」です。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾







コメントをお書きください