この土日は学年末テスト前ということで教室の方も臨時開校！

生徒たちは全員が4～5時間ほど勉強してくれて、クタクタになりながらも充実感に満ちた表情で帰っていきました(^^)

さて、そのテスト勉強をしている中で、ある生徒がおうぎ形の面積を求める公式について疑問をぶつけてきてくれたので、今日はその疑問を解決してみたいと思います。

おうぎ形の面積は、

「母線の長さ × 弧の長さ ÷ 2」

という公式で求めることが出来るのですが、その生徒は

「確かこう教わった気がする。あれ？こうじゃなかったっけ？わからん。けどなんとなくこの計算でやってた。」

という感じで、それが正しいかどうかの確証すらないまま使っていたようです(^^;

で、その生徒の疑問というのは、なんで母線の長さと弧の長さを掛けて 2 で割ると面積になるの？、ということでしたので解説してみます。

まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。

母線 x と中心角 θ が分かっている場合、おうぎ形の弧の長さを求める式は次のようになります。

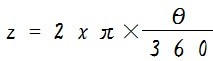
この式を利用して、母線 x と弧の長さ z が分かっていて中心角 θ を求める式を作ると次のようになります。

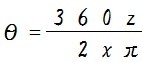
で、扇形の面積は、母線 x と中心角 θ が分かっている場合、式で表すと次のようになります。

（おうぎ形の面積を A とします）

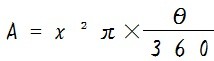
ですが、この式では中心角が分からないと面積は求められないですよね。

けれど、母線 x と弧の長さ z が分かっていれば中心角 θ を求める式が作れましたよね？

なので、これを面積を求める式に代入してみます。

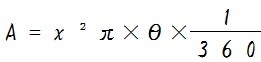
これで中心角が分からなくても母線 x と弧の長さ z さえわかればおうぎ形の面積を求められます。あとはこの式を整理すると、、、

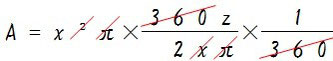
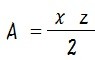
よって、おうぎ形の面積は 「母線の長さ × 弧の長さ ÷ 2」 で求めることができるというわけですね。