今日、生徒が苦戦していた円錐の表面積の求め方について簡単に書いてみたいと思います。

x と y の長さが分かっていて表面積を求めなさい、っていう問題ですね。

立体図形の表面積を求める問題は、立体を平面に、平面を立体に、その図形のイメージを正しく捉えられるか、っていうのが一つのポイントだと思います。

円錐の場合、展開すると、

こんな感じで、おうぎ形と円がくっついた形になります。

それぞれの面積を求めて足せばいいですね。

円の方は 「半径×半径×π」 なので 「ｙ²π」 となります。

おうぎ形の方は、「おうぎ形の弧の長さ」 ÷ 「母線 x を半径とする円の円周」 で円に対するおうぎ形の割合を計算し、円全体の面積からその割合分の面積を求めます。

ちなみに 「おうぎ形の弧の長さ」 は 「半径 y の円の円周」 と同じ長さなのでそこから計算します。

あとはこの二つを足せば円錐の表面積を求めることが出来る、というのが考え方ですね。

さて、ではここで一歩進んで 「もっと楽に求める方法」 について考えてみましょう(^^)

まずは上記の考え方を x と y を使って一つの式として書き出します。（円錐の表面積を A としてます）

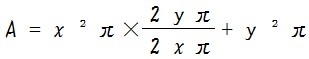
この式を整理すると、

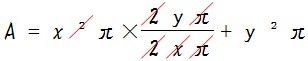
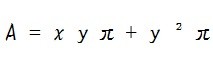
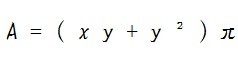
実はこんなに簡単に円錐の表面積を求めることが出来るんですね。

中学一年生の一学期に習った代数の計算を利用すれば複雑な計算も楽に解けてしまうわけです(^^)

とはいえ、この公式を生徒に教えることはしません。

テストの成績を伸ばすことだけが目的ならそれでいいかもせれませんが、本当に伸ばさないといけないのは学ぶ力、考える力です。

子どもたちには、何も考えずただ公式に当てはめて計算をするだけではなく、元となる考え方をきちんと理解してほしいと思っています。